summary <- group_by(data, device) %>%
summarise(
mean_download = mean(Download, na.rm = TRUE),
sd_download = sd(Download, na.rm = TRUE),
mean_upload = mean(Upload, na.rm = TRUE),
sd_upload = sd(Upload, na.rm = TRUE)
)
print(summary)Hyperoptic internet speed
The past week or so has been full of troubleshooting wifi speed problems. Various changes suggested by the Hyperoptic team has not succeeded in bringing my internet speed close to the speed of 1 Gbps promised in the package I chose.
Most recent suggestion was that I try doing the speedtest on different devices. Perhaps the experts at hyperoptic are baffled their suggestions of trying a different cable or resetting the router are not working. The trouble must be with my device! So this is what I did.
However, I wondered, how will they know if the difference in speed between different devices is significant? Worry not, Hyperoptic, I was trained in statistics, and my passion for R can help us both.
You are welcome.
About the data
The data used for this report were collected between 17/05/2024 19:00 and 18/05/2024 01:00. All deviced were connected to the 5 Ghz band. I have not tested the speed on the 2.4 Ghz band.
The variable device in the dataset refers to one of three devices available to me at the time of testing: personal laptop, phone, and work laptop. I was not able to conduct the speedtest on my TV because despite being connected to wifi it shows the ‘no internet’ error message.
Create a summary of data
The average speed per device are:
| download (± SD) Mbps | upload (± SD) Mbps | |
|---|---|---|
| personal laptop | 275 (±91.6) | 114 (± 60) |
| phone | 204 (±40.4) | 172 (± 45) |
| work laptop | 275 (±102) | 157 (±49) |
Averages are calculated for 10 measurements per device. Standard deviation values are denoted by ±.
Visualise data
@boxplot is a visualisation of the values summarised above.
data_melted <- melt(data, id = "device")
ggplot(data = data_melted) +
geom_boxplot(aes(x = device, y = value, fill = variable)) +
xlab("device") +
ylab("speed (Mbps)") +
labs(fill = "speed measured") +
scale_fill_manual(values = c("lightblue1", "thistle2"))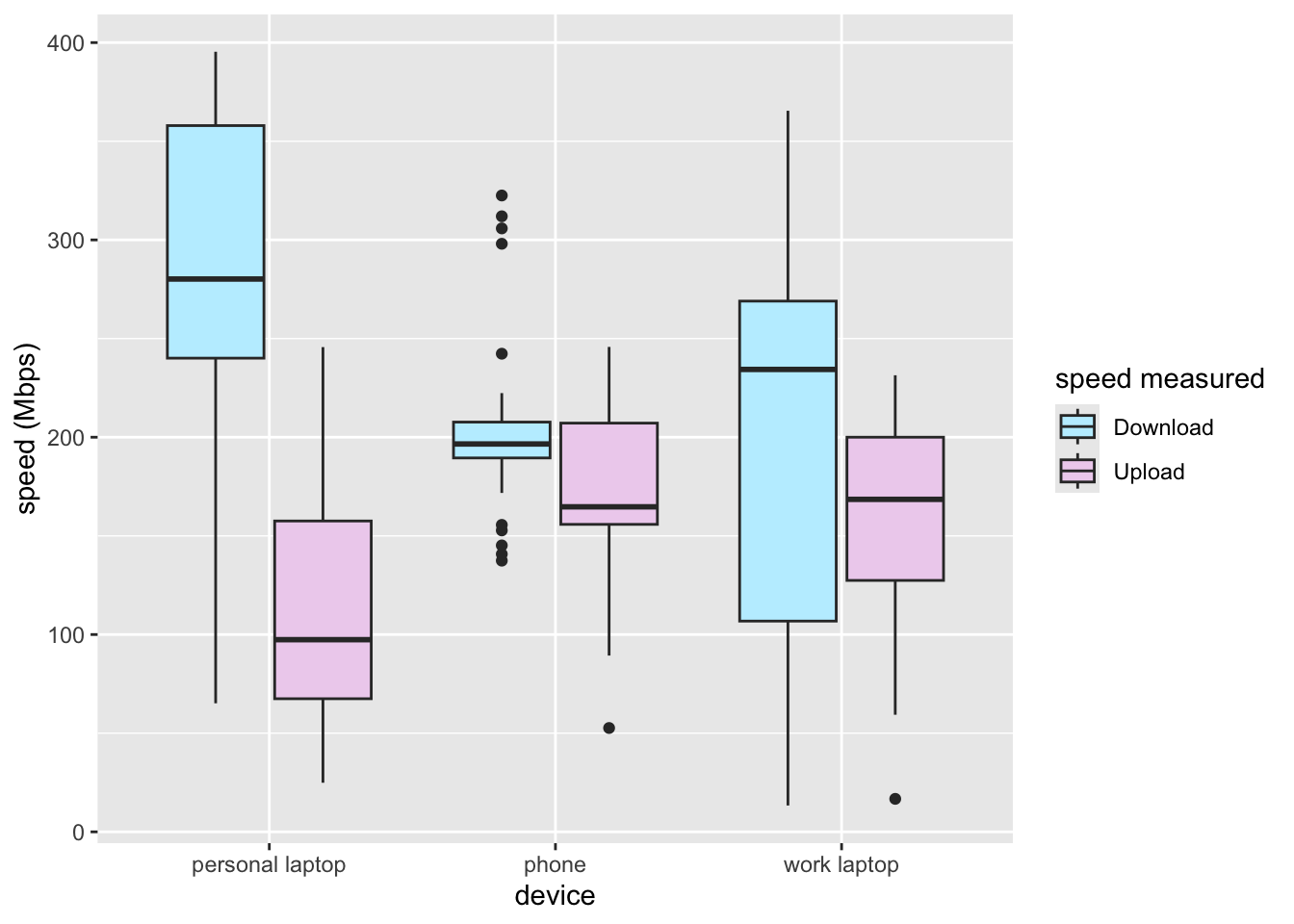
Test the normality of data
Next I conducted Shapiro test to check normality of data. Non-significant p-values (greater or equal than 0.05) indicate the data is normally distributed.
Download speed:
res_download <- aov(Download ~ device, data = data)
normal_download <- shapiro.test(res_download$residuals)
print(normal_download)
Shapiro-Wilk normality test
data: res_download$residuals
W = 0.95476, p-value = 0.0006292The p-value of Shapiro test is 6.3^{-4}, meaning the data is not normally distributed.
Upload speed:
res_upload <- aov(Upload ~ device, data = data)
normal_upload <- shapiro.test(res_upload$residuals)
print(normal_upload)
Shapiro-Wilk normality test
data: res_upload$residuals
W = 0.98951, p-value = 0.5175The p-value of Shapiro test is 0.51746, meaning the data is normally distributed.
Check homoscedascidity of data
Conduct Levene’s test to check for homoscedascidity of data.
Download speed:
homoscedasticity_d <- leveneTest(Download ~ factor(device),
data = data)
print(homoscedasticity_d)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 13.133 7.445e-06 ***
113
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Levene’s test is significant, meaning variances of download speed data across different devices are not equal.
Upload speed:
homoscedasticity_u <- leveneTest(Upload ~ factor(device),
data = data)
print(homoscedasticity_u)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 1.3719 0.2578
113 Levene’s test is non significant, meaning our data is homoscedastic (i.e. variances of upload speed data across different devices are equal).
ANOVA
Assumptions
The assumption of:
- Normality of data has been met for upload speed but not for download speed- i.e. only upload speed values are normally distributed.
- Homoscedasticity has been met for upload speed but not for download speed- download speed values have unequal variances between types of device.
- Independence of samples has been met.
Download speed values violate two of the assumptions of ANOVA, however at this point I don’t have the determination to research bootstrapping methods to corect for this, so i will just proceed with the ANOVA.
Analysis of variance (ANOVA)
Download ANOVA
print(report(res_download))For one-way between subjects designs, partial eta squared is equivalent to eta squared.
Returning eta squared.The ANOVA (formula: Download ~ device) suggests that:
- The main effect of device is statistically significant and medium (F(2, 113) = 8.31, p < .001; Eta2 = 0.13, 90% CI [0.04, 0.22])
Effect sizes were labelled following Field's (2013) recommendations.Upload ANOVA
print(report(res_upload))For one-way between subjects designs, partial eta squared is equivalent to eta squared.
Returning eta squared.The ANOVA (formula: Upload ~ device) suggests that:
- The main effect of device is statistically significant and large (F(2, 113) = 12.05, p < .001; Eta2 = 0.18, 90% CI [0.08, 0.27])
Effect sizes were labelled following Field's (2013) recommendations.ANOVA results
There was a main significant effect of device type on both upload and download speed.
To investigate which devices were significantly different from each other I conducted a post hoc test.
Turkey HSD test
Download Turkey
post_test_d <- glht(res_upload,
linfct = mcp(device = "Tukey")
)
print((summary(post_test_d, test = univariate())))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = Upload ~ device, data = data)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
phone - personal laptop == 0 58.32 12.06 4.837 4.21e-06 ***
work laptop - personal laptop == 0 42.56 12.06 3.530 0.000603 ***
work laptop - phone == 0 -15.76 10.93 -1.441 0.152237
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Univariate p values reported)Upload Turkey
post_test_u <- glht(res_upload,
linfct = mcp(device = "Tukey")
)
print((summary(post_test_u, test = univariate())))
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = Upload ~ device, data = data)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
phone - personal laptop == 0 58.32 12.06 4.837 4.21e-06 ***
work laptop - personal laptop == 0 42.56 12.06 3.530 0.000603 ***
work laptop - phone == 0 -15.76 10.93 -1.441 0.152237
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Univariate p values reported)Interpretation of results
According to the resulrs of Turkey test:
There is a significant difference in download speed between
personal laptop and phoneand betweenpersonal laptop and work laptop. However, the comparison betweenphone and work laptopis not significant.Similarily, there is a significant difference in upload speed between
personal laptop and phoneand betweenpersonal laptop and work laptop. However, the comparison betweenphone and work laptopis not significant.
Therefore it seems like the type of device does have an effect on upload and download internet speed.
None of the measurements however come close to the 1 Gbps that my Hyperoptic package was supposed to provide, therefore in non-statistical terms I would conclude that:
Best wishes,
Julia